日志
科普:摩擦力与走路力学总结(4)
热度 2 |||
在《继续分析刘延柱教授走路力学》一文中,我从第一原理出发(First Principle) 计算了人走路时当一脚已经离地时,另一只脚与地面摩擦力大小,得出的公式是
其中 m 是人体质量, v为步行速度, L为腿长, g 为重力加速度,[ix]\theta[/ix]为腿与垂直线的夹角 。上式除以人体重量 mg, 我们得出单位重量的摩擦力 f 为

[ix]F= m\sin\theta[g(3\cos\theta-2) - v^2/L][/ix]
[ix] f = \sin\theta \left( 3\cos\theta-2 - v^2/gL\right) [/ix]
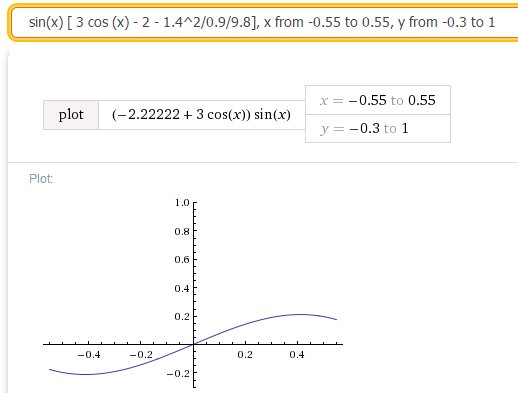
代入人的平均步行速度 1.4米/秒,腿长L=0.9米,g=9.8m/s^2,我们得出摩擦力随角度的变化 如下图


从图中可以看出,按普通速度步行,当一脚着地、一脚离地时:(1) 水平摩擦力最大约为体重的20%;(2)当着地的腿与地面垂直时水平摩擦力为0;(3)摩擦力在腿垂直前后方向发生改变。
有人可能会问了,当腿与地面垂直时,法向力最大,为什么摩擦力是零呢,摩擦力 = 法向力 X 摩擦系数 难道不是吗?
The answer is NO!
摩擦力 = 法向力 X 摩擦系数 那是指滑动摩擦而言。走路没有打滑的时候,摩擦力是静摩擦,静摩擦大小是从0到一个最大值。这是初中物理。
另外一点值得注意的是,因为无打滑走路时摩擦力是静摩擦,并没有因为摩擦力而造成的动能损失,人体质心水平速度基本是恒定的,而不是不断的启动、停止。能量损失主要来自人体质心的上下起伏,这个能量损失可以视为人体与地面在垂直方向的非弹性碰撞。由此可见,走路是一种相对高效的移动,一个人吃一顿饭可以走相对长距离就是这个道理。
注意上面计算出来的摩擦力大小中根本没有出现摩擦系数,但我们假定没有打滑。如果静摩擦系数太小,不足以提供这么大的静摩擦力,那么我们的假设不能成立,走路就会出现打滑现象。
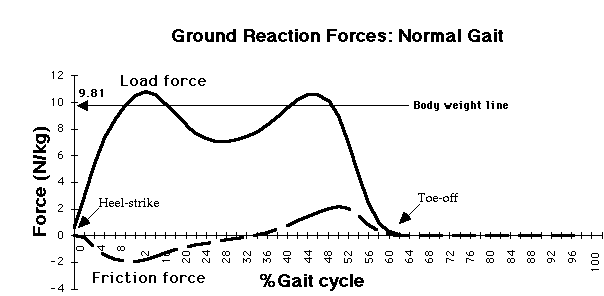
对比下面的实验数据,以上三点完全吻合: 下图中重量线在9.8,而摩擦力最大约2,因此摩擦力约为重量的20% 。

对刘延柱论文的评价:
1. 刘延柱计算的水平力在小角度近似正确
刘延柱的论文中水平力为 [ix]F = K \theta[/ix],这是一个角度很小时的近似,而且K是其论文中一个未知参数。但他这个结果还是抓住了上面三点中的两点,垂直时水平力为0,水平力方向改变。
2. 刘延柱计算的步长上限
刘延柱也正确理解了静摩擦概念,在其论文中得出最大步长 [ix]2 d < 2 \mu L[/ix],也就是小于静摩擦系数乘以腿长。摩擦系数为零时,步长当然为0。但注意,刘的计算仅仅得出了一个上限,而不是步长的值。
而我在《科普:走路的初中物理》中得出的步长公式为 [ix]D=2L\frac{ \mu}{\sqrt{1+\mu^2}}[/ix],可见刘的上限只在静摩擦系数较小时才近似为理论步长。
3. 给刘延柱论文打分: 40/100 (不及格)
+ 小角度时定性分析正确,正确理解了静摩擦概念
- 对于这么个牛顿力学问题,未能从第一原理出发进行计算,这是大大的失分。
针对网上其他放大炮而缺乏计算的说法
我的建议是, go back to middle school and get some education.







