日志
日夜的方程
热度 3 ||
夏日炎炎。在网上偶尔看到一篇英文提到中国古代天文学,里面有个词“Winter Extreme"。顾名思义这是中文的”冬至”,英文叫 Winter Solstice。我之前一直想当然地认为“冬至”是冬天来到的意思。难道这个“至”确实是至极之意?查阅之后发现确实如此。《后汉书-律历志》注解中写道:“冬至之为极有三意焉:昼漏极短,去极极远,晷景极长。极者,至而还之辞也。” 冬至是白天时间最短的一天。还对极点给出了数学直觉极好的定义:到了然后返回之点 。Solstice 一词来自拉丁文,意思是太阳在天球上的纬度看起来不变之意。用数学术语来说,相当于一个曲线顶部的平坡处(导数为零)。殊途同归。冬至一词这个至字的含义我这才弄清楚,还是看了英文翻译才幡然醒悟。感觉需要继续思考一下相关问题了。
且让我们根据基本天文知识--地球自转的同时绕太阳公转---来写个数学公式,计算每天太阳升起与落下的时间,阳光投射角度随时间的变化等等。要做这个计算,需要先确定坐标。那么就让我们以冬至这点的状态设置坐标,然后开始计算。下图中,O是地球的球心,N是北极,S为南极,地球绕 NS 轴自转,P为地球表面一点; A 为太阳所在,但应该想象太阳在右边无限远处,阳光是平行的,方向是从A到地心的连线;地球绕太阳的轨道是在水平面上,DOE 线垂直于轨道平面;地球自转轴与 DOE 线的夹角为 $\beta$,就像个倾斜的陀螺。冬至日的时候,NOAD 四点在同一个面上,垂直于地球轨道平面。此时,地球自转轴与阳光的夹角 <NOA 就是地球自转倾角 $\beta$ 加上90度。计算 OP 与阳光 的角度 $\theta$ 是一个相当直接的几何问题。坐标设置如下图中的 XYZ 与 X'Y'Z'。
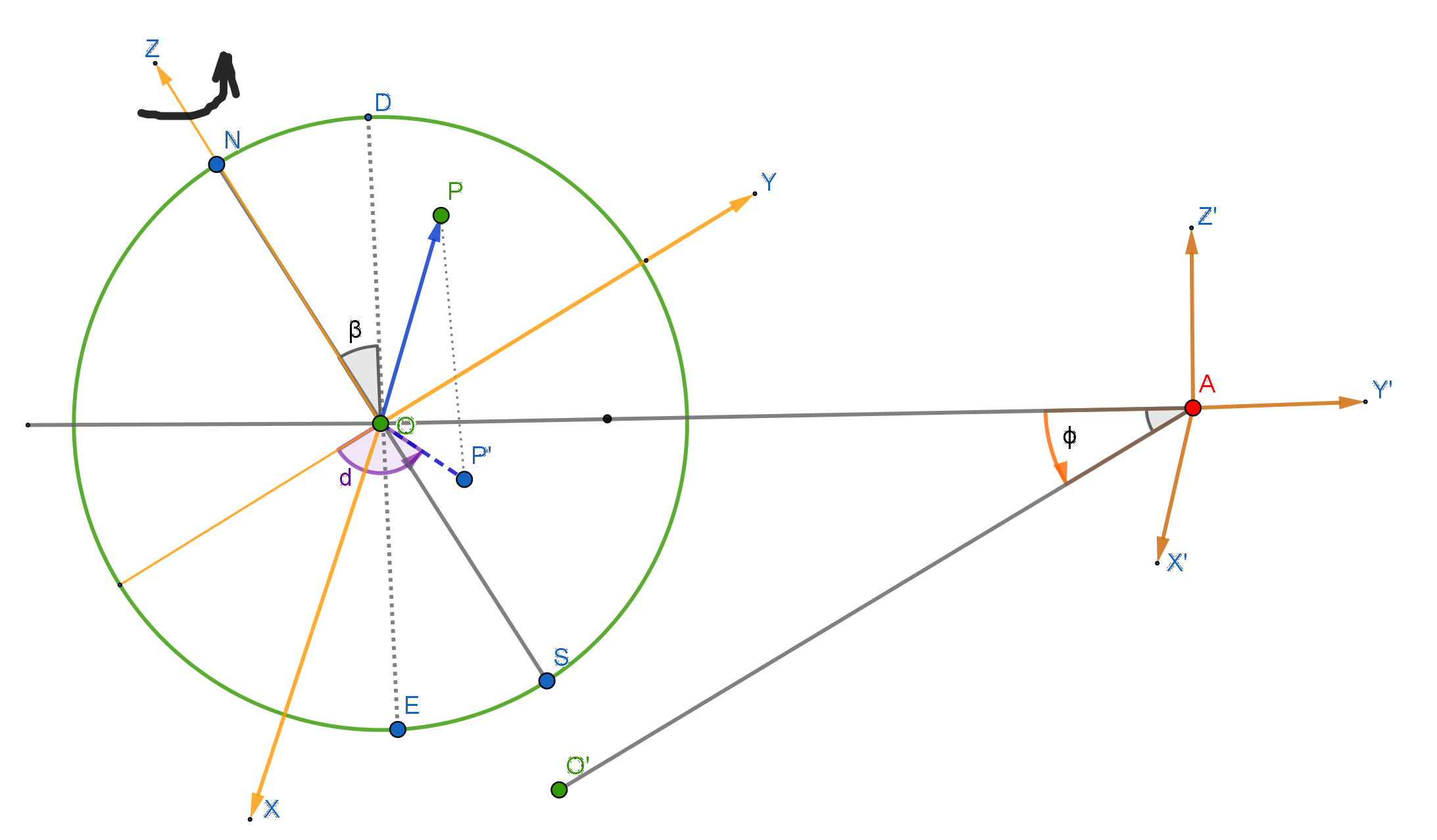
上图中,设P点的纬度为 L,P在XY平面上的投影为 P', OP' 与 -Y 轴角度为 d 。阳光方向 为AO 。在XYZ坐标系里,OP的方向为 $(\cos L \sin d, -\cos L\cos d, \sin L)$,而OA方向为$(0,-\cos\beta, \sin\beta)$。
我们有
$\cos\theta = \cos\beta \ \cos L \ \cos d + \sin \beta \ sin L $
太阳升起与落下时,OP 与阳光角度垂直,$cos\theta=0$. 所以, 日出、日落的方程是:
$ \cos\beta \ \cos L \ \cos d + \sin \beta \ sin L=0$
也就是说
$\cos d = -\tan \beta \tan L$
从上面方程求解出 d 也就知道了这天太阳升起的时间。以北京为例, 纬度L约为 40度,代入地球轨道倾角 23.43688 度,解出 d = 111.33 度。地球每小时转15度,因此这天的太阳升起的时间是 111.33/15 = 7.42 (小时),也就是7点25 分。日落时 角度为 270-21.33,日落时间因此是 (270-21.33)/15 =16.6,也就是下午4点多。
另外,上面的方程并不见得总是有解。对于高纬度地区,右边的绝对值完全可以大于1。这对应于两极地区极昼或者极夜的情况。
冬至点之后,地球继续绕太阳转动,到了O' 的位置。跳出太阳系看世界,地球自转轴NS的方向不变,但是阳光方向变成了 AO' 方向,NO'AD 四点不再在一个平面上,地球自转轴与阳光的夹角 <NO'A 也变了。怎么办?
如果想继续使用上面的公式,我们需要首先计算出夹角 <NO'A,然后用这个角度减去90度, 得出的 $\beta^\prime$,然后代入上面的$\sin d$ 公式如法炮制。这相当于把地球翻转成上图冬至时的情形(但 DOE不再垂直于轨道平面)。从上图中可以看出
$\sin\beta^\prime = \cos\phi\ \sin\beta$
从这个公式可见,从冬至点起,地球在绕太阳轨道运行90度之后,地轴与阳光方向垂直 (公式右边因为 cos 项为零,因此 $\beta^\prime =0$) 。日出方程成为 $\sin d=0$。此日昼夜长度相等,古代中国称为春分。西方称为 Equinox (意思是昼夜相等)。
综合起来,我们的日出方程为
$\cos d = -\tan[\sin^{-1}(\cos\phi\sin\beta)]\tan L = -\frac{\sin\beta\cos\phi\tan L}{\sqrt{1-\sin^2\beta\cos^2\phi}}$
上面的结果看起来不错,但有一个问题。计算是把地球移到轨道的某一处,然后假设地球在原处转动,计算从夜中开始到凌晨的转角。但是正确的计算应该考虑地球在自转的同时还在公转。我们希望得到的是一个含时间的方程,同时考虑自转与公转。如上所述,在XYZ坐标系中,OP的方向为 $(\cos L \sin d, -\cos L\cos d, \sin L)$。而在X'Y'Z'坐标系中,AO'方向为 $(\sin\phi, -\cos\phi, 0)$。要计算两者的角度需要找出两个坐标之间变换关系。这是一个角度为 $\beta$的转动。我们有
$\hat{x} = \hat{x^\prime}\\
\hat{y}=\cos\beta \ \hat{y^\prime} +\sin\beta \ \hat{z^\prime}\\
\hat{z} = -\sin\beta \ \ \hat{y^\prime} + \cos\beta \ \hat{z^\prime}$
代入计算OP 与 O'A 之间的角度,我们得到
$\cos\theta = [\cos d \ \cos L \cos\beta + \sin L \sin\beta] \cos\phi + \sin\phi \sin d \cos L$
设地球自转角速度为 $\omega$, 公转角速度为 $\Omega$, t 为时间,则 $d = \omega \ t $, $\phi=\Omega \ t$。
因此太阳与直立标尺的角度 $\theta$ 的方程为
$\cos\theta = \left[ \sin L \sin\beta + \cos L \cos\beta \ \cos (\omega \ t) \right]\ \cos (\Omega\ t) + \cos L \sin (\omega\ t) \sin(\Omega\ t) $
至此,我们得到计算日出、日落时间的方程是:
$\left[ \sin L \sin\beta + \cos L \cos\beta \ \cos (\omega \ t) \right]\ \cos (\Omega\ t) + \cos L \sin (\omega\ t) \sin(\Omega\ t) =0$
或者:
$
\frac{ \sin L \sin\beta + \cos L \cos\beta \ \cos (\omega \ t)}{\cos L \sin (\omega\ t)}=-\tan\Omega t
$
其中 L 为 纬度,$\beta$ 为行星自转倾角(地球约23.5 度),$\omega$ 为行星自转角速度,$\Omega$ 为行星公转角速度,时间是从冬至算起。当然上述计算中假定轨道是圆形,如果是实际椭圆轨道,那方程将复杂些。另外,空气折射也没有考虑。
要解这个方程一时也看不出有什么可以简化,似乎只能用蛮力。这正是计算机的长处。对比两种方法,以北纬40度为例计算从冬至半夜 (d=0) 到天明的时间,后一种晚约一分19秒,这是一个不可忽略的差别。这也说明第一种计算存在相当的缺陷。
文末PYTHON代码计算了北纬40度365天的日出、日落时间。
附:代码
# -*- coding: utf-8 -*-
"""
Created on Fri Jul 8 21:00:50 2018
@author: YDX
"""
from sympy import symbols, cos, sin, acos, pprint,diff,solve,nsolve, Eq, latex, integrate,pi, simplify, Matrix
from sympy.plotting import plot
import matplotlib.pyplot as plt
import numpy as np
import sympy as sym
# alpha -- angle between sun ray and tilt axis
# tilt -- titl axis
# phis -- angle around sun
tilt, phis, d, lat, sp, t = symbols(' tilt phis d lat sp t')
# z^ = cos(tilt) z'^ - sin(tilt) y'^
# y^ = sin(tilt) z'^ + cos(tilt) y'^
# x^ = x'^
# sun ray: [sin(phis) x'^, - cos(phis) y'^,0]
#point: [cos(lat)*cos(d), cos(lat)*sin(d), sin(lat)]
m = sym.zeros(3,3)
m[0,0]=1
m[1,2] = sin(tilt)
m[1,1] = cos(tilt)
m[2,1]= -sin(tilt)
m[2,2]= cos(tilt)
print(m)
loc = Matrix([cos(lat)*sin(d), -cos(lat)*cos(d), sin(lat)])
print("loc=",loc.shape, loc)
ray = Matrix([sin(phis), - cos(phis),0])
loc_sun = sym.Transpose(m) * loc
print(loc_sun.shape, loc_sun)
dotp = sym.Transpose(ray)*loc_sun
#print(dotp.shape, dotp)
dot=simplify(dotp[0,0])
print("dot=",dot)
sp = acos(dot)
print("angle", sp)
print(latex(sp))
dlen= 23+56/60+4/3600
ylen = 365.2422
oe = 2*np.pi * 24/dlen
os = 2*np.pi/ylen
d2rad = np.pi/180
til = 23.43688*d2rad
lati = 40/180*np.pi
def angle(t, tilt, lat):
d = oe *t
phis = os *t
return np.arccos((np.cos(d)*np.cos(lat)*np.cos(tilt) + np.sin(lat)*np.sin(tilt))*np.cos(phis) + np.sin(phis)*np.sin(d)*np.cos(lat))
ts=np.arange(0,365,0.005)
angles = angle(ts, til, lati)
plt.plot(ts[angles>np.pi/2], angles[angles>np.pi/2])
spd =sp.subs({lat:lati, tilt:til, phis:os*t, d:oe*t})
print(latex(spd))
sols=[]
day=0
lasts=0
intv = 0.2
a1 = np.arccos(-np.tan(til)*np.tan(lati))
d1=nsolve(Eq(spd,np.pi/2), t, 0)
d2=nsolve(Eq(spd,np.pi/2), t, d1+0.4)
d1=nsolve(Eq(spd,np.pi/2), t, 0)
d3=nsolve(Eq(spd,np.pi/2), t, 1)
print (d1,d2,d3, d1*24, d2*24, (d2-d1)*24, (d3-d1)*24)
d5= d1*oe
print ("diff=", a1, a1/d2rad, d5, (d5-a1)*24*60/oe)
lasts=0
#lasts = nsolve(Eq(spd,np.pi/2), t, [lasts+0.01,lasts+intv], solver='bisect')
#print (lasts)
raise SystemExit
while lasts<365:
try:
lasts = nsolve(Eq(spd,np.pi/2), t, [lasts+0.0001,lasts+intv], solver='bisect')
sols.append(lasts)
intv = 0.4
#print ("Found " +str(lasts))
except:
#print ("no solution", lasts, lasts+intv)
lasts = lasts+intv
days = np.array(sols)
sz = days.size
if(sz%2):
sz = sz-1
nd=np.reshape(days[0:sz], (-1,2))
print(nd)
发表评论 评论 (5 个评论)

- 回复 lfyhao
- 杜甫先生有首诗写冬至,写的是冬至这天达到至阴,阴极而阳生。其中有一句“吹葭六管动飞灰”是描写我们的先人们如何测量冬至的时间点,我们的先人那时候对音律的认识是六阶,他们就按音律弄六个长短不一的管子,里面放竹子内膜烧烧成的灰,在冬至日埋在半地下,当冬至的时间点来临时,阳气生发,里面的灰就会飞动起来,飞动的那个时刻点就是冬至的时间点。这个时候太阳正射南回归线。

- 回复 岳东晓
lfyhao: 杜甫先生有首诗写冬至,写的是冬至这天达到至阴,阴极而阳生。其中有一句“吹葭六管动飞灰”是描写我们的先人们如何测量冬至的时间点,我们的先人那时候对音律的 ...
 看来我这个“冬天来了”凸显出读杜工部不够啊
看来我这个“冬天来了”凸显出读杜工部不够啊








 起文科生
起文科生 